[ML] Linear Regression

#1 Concept of Linear Regression

▶ Linear Regression(선형 회귀)의 개념

공부 시간에 따른 학생들의 점수를 나타낸 표(=Training data)

이 데이터를 가지고 학습을 하여 모델을 생성하여 학습을 하는 것이 Linear Regression이다. Regression은 학습된 데이터를 기반으로 새로운 데이터를 예측한다.(공부 시간 데이터들을 학습하여 성적을 예측)

​- Regression Data(X값, Y값): X값(예측을 하기 위한 자료), Y(정답 값)

​

▶ (Linear) Hypothesis(가설)

: 직선의 가설을 세우는 것이 Linear Hypothesis, 어떤 데이터가 존재한다면 그에 맞는 선(함수)을 찾는 것.

H(x)는 W, b에 따라 값이 달라짐.

어떤 가설이 좋은지 판별할 수 있는 것 == 손실(실제값과 예측값의 차이)

손실 함수를 통해 우리가 세운 가설과 실제 데이터의 차이를 알 수 있음

 

▶ Cost Function(손실 함수, 오차 함수)

​: H(x)를 위의 cost에 대입.

 

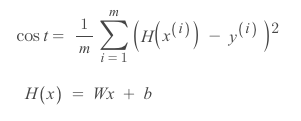
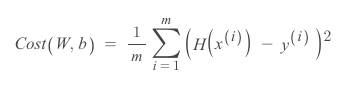
: 결국 Cost Function은 W,b의 값에 따라 달라짐

​→ 손실함수의 목표 : cost(오차)를 최소화하는 W,b를 구하는 것.

​

▶ Tensorflow Linear Regression 구현 코드 참고

https://github.com/ChoiJiA/DeepLearning_Study/blob/master/code/Section2_1_Linear_Regression_Placeholder.ipynb 

GitHub - jiachoi-ds/Machine-Learning: Machine Learning(Deep Learninig) Study

 

 

#2 Minimize Loss Funcion of Linear Regression 

▶ Hypothesis and Cost Function

· cost funcion : 실제 값과 가설의 값의 차이를 나타내주는 함수. (m : 데이터의 개수)

▶ Simplified hypothesis(가설을 단순화 하여 손실함수를 이해해보겠습니다.)

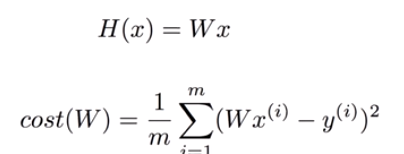
H(x) 함수에서 b를 생략. (기존, H(x) = Wx + b), cost도 W와 관련된 함수로 간소화.

가지고 있는 데이터(X,Y)

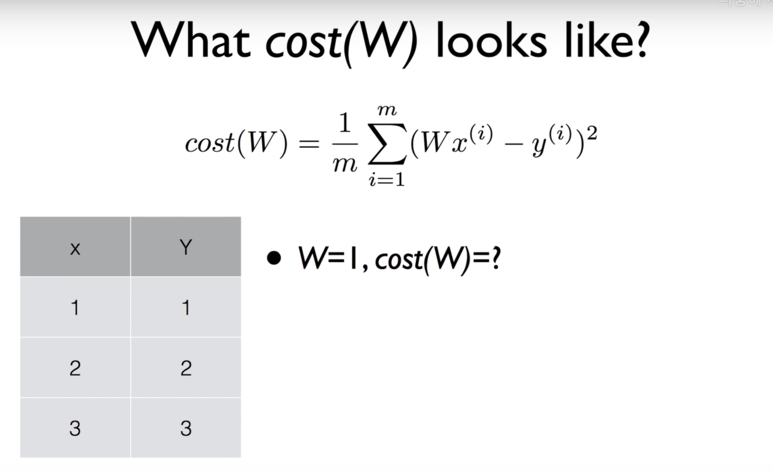
→ W = 1, cost(W) = ? (Cost식에 대입)

1/ 3 { (1 * 1 - 1)^2 + (1 * 2 - 2)^2 + (1*3 - 3)^2 } = 0

cost(W) = 0

→ W = 0, cost(W) = ?

1/ 3 { (2 * 1 - 1)^2 + (2 * 2 - 2)^2 + (2*3 - 3)^2 } = 0

cost(W) = 4.67

→ W = 2, cost(W) = ?

1/ 3 { (3 * 1 - 1)^2 + (3 * 2 - 2)^2 + (3*3 - 3)^2 } = 0

cost(W) = 4.67

= 손실함수 : 위의 가중치에 따른 값의 변화식을 참고하여 모든 값들을 대입하여 만들어진 함수의 모형.

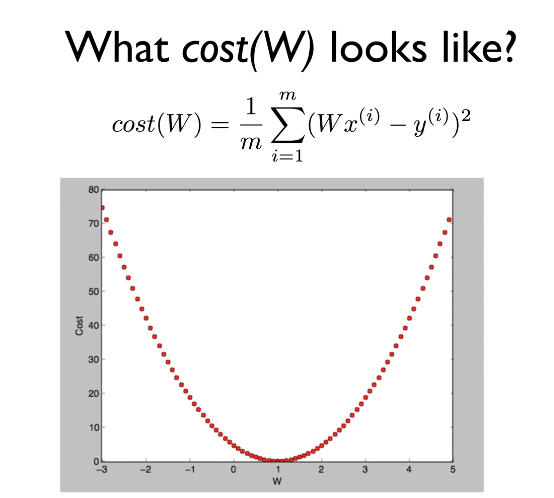
※※ 손실함수를 최소화하여 실제값과 예측값의 차이를 최소화 하는 것이 목표!

→ 손실함수가 최소화 되는 지점의 가중치 값(W)을 찾아야 함. (위의 그림에선, W=1)

이를 기계적으로 찾아내기 위한 알고리즘 : Gradient Desent Algorithm

 

▶ Gradient Desent Algorithm(경사 하강 알고리즘)

- 주어진 손실함수를 최소화하는데 사용되는 알고리즘

- W, b를 최소화하는데 도움이 됨.(많은 값들이 있는 cost function을 최소화 하는데도 도움이 됨)

→ 어떠한 방식으로 최저점을 찾을수 있을까?

: 경사 각도를 따라 움직이며, W를 바꾸며 최종적으로 경사가 0인 지점에 도달하는 것(손실 최소화 지점).

(경사=기울기, 미분을 하며 구함)

가중치 업데이트 수식. 기존의 가중치에서 상수(알파, 학습률)에 손실함수의 미분 값을 곱한 것을 빼며 가중치를 조정한다.

최종 Gradient Desent Algorithm 수식. 이 식에 대입하여 가중치를 갱신하여 손실함수의 최소값을 찾을 수 있다.

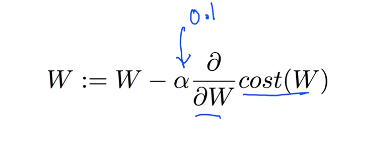
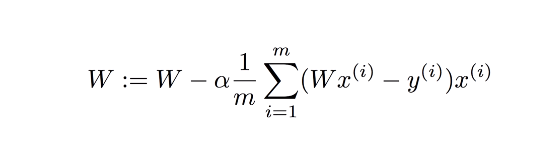
▶Tensorflow 구현 코드 참고

GitHub - jiachoi-ds/Machine-Learning: Machine Learning(Deep Learninig) Study

 

#3 Multiple features of Linear Regression 

▶ Review

- Hypothesis ; H(x) = Wx + b

- Cost function(실제값과 예측값의 차이를 최소화하기 위한 함수)

- Gradient Desent Algorithm(Cost를 최적화하는 w,b의 값을 찾기 위한 알고리즘)

 

▶ 여러 feature의 Linear Regression

1. Hypothesis (학습해야 할 값이 많아짐)

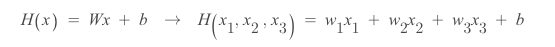
2. Cost function

값이 많아질 경우 이러한 형태로 가정함수를 변화시켜야 한다. --> 값을 계속 바꿔야 하기 때문에 편하기 하기 위해 --> Matrix 사용

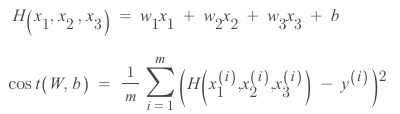
3. Matrix(행렬)로 함수를 표현

여러 값을 곱할 경우의 행렬식(instance는 1개)

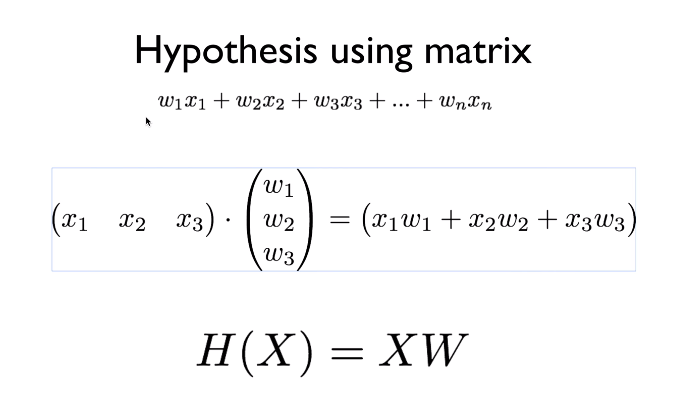
: matrix(행렬) --> 여러 값 한 번에 계산 가능.

인스턴스가 많을 경우 전체를 긴 매트릭스 형태를 가중치를 곱하는 형태로 행렬식을 사용할 수 있음.

▶ WX vs XW

- 이론상으로는, H(x) = Wx + b의 형태를 사용.

- 구현시에는, H(x) = XW(행렬 사용), 행렬을 사용한 가설함수의 형태를 쓴다.